В печати: Изв. Самар. Науч. центра РАН. 2005.

© 2005 С.С. Крамаренко
Николаевский государственный аграрный университет
ул. Парижской коммуны, 9, г. Николаев, 56021, Украина (kssnail@rambler.ru)

В последнее время появилось много публикаций, в которых продемонстрированы возможности применения энтропийно-информационного анализа (ЭИА) в различных областях биологической науки [1-3], физиологии и медицине [4-6] и др. В экологии, наряду с использованием формулы К.Шеннона для оценки меры биоразнообразия отдельных сообществ и биоценозов, ИЭА получил свое применение и в качестве метода биоиндикации экосистем по соотношению мер адаптивности и инадаптивности признака или группы признаков [7-8]. При этом приводятся многочисленные примеры применения ЭИА при изучении как дискретных (качественных) признаков, имеющих полиномиальное распределение (для которых исходно были разработаны основные положения теории информации и, в частности, ЭИА), так и количественных (полигенных), которые чаще всего подчиняются нормальному закону распределения или близкому к нему.

Однако до сих пор нет единого, теоретически обоснованного метода оценки энтропии для количественных признаков. Кроме того, проанализировав примеры применения ИЭА и методики, которые используются в этих работах, мы пришли к заключению, что они очень часто имеют один существенный недостаток, который может повлиять на получаемые результаты. Это побудило нас к разработке нового подхода к использованию ИЭА в применении к количественным признакам.

Базисным понятием теории информации является понятие энтропии, математически точный смысл которого вытекает из работ К.Шеннона [9]. Энтропия – мера неопределенности некоторой ситуации. Ее также можно рассматривать в качестве меры рассеяния, и в этом смысле она подобна статистическому понятию “дисперсия”. Но если дисперсия является адекватной мерой рассеяния только для специальных распределений вероятностей случайных величин (в частности, для гауссова распределения), то энтропия не зависит от типа этого распределения. Кроме того, энтропия обладает и рядом других полезных свойств. Во-первых, неопределенность любой системы возрастает с ростом числа возможных исходов. А, во-вторых, мера неопределенности обладает свойством аддитивности.

Впервые особенности функционирования биологических систем разного уровня с точки зрения теории информации были рассмотрены в работе И.И.Шмальгаузена [10]. Им были введены понятия о каналах прямой и обратной связи, по которым передается генетическая и фенотипическая информация, рассмотрены закономерности кодирования и преобразования биологической информации.

У.Эшби [11] впервые предложил использовать понятие энтропии для характеристики меры сложности системы. Согласно его представлениям, сложность системы (в том числе и биологической) можно охарактеризовать ее разнообразием. Под разнообразием обычно понимается количество состояний, которое может принимать система. Кроме этого, при оценке энтропии учитывается не только абсолютное количество таких состояний, но и вероятность (а в выборочных исследованиях вероятность можно заменить частотой), с которой система принимает то или иное состояние. Тогда оценкой для энтропии может служить выражение:

где p_i – вероятность (или частота) того, что система примет i-тое состояние из k возможных.

Как легко убедиться, максимума эта величина достигает в том случае, когда вероятности принятия системой любого из k возможных состояний равны. В этом случае значение энтропии для такой системы будет равно:

В том же случае, когда система может принять только одно состояние с частотой равной 1, энтропия ее равняется нулю. Таким образом, для любой (невырожденной) системы имеет место выражение:

Энтропия, как мера разнообразия и организованности системы, прежде всего, характеризует степень ее неопределенности или, другими словами, детерминированности. Система считается тем детерминированее, чем меньше ее значение энтропии, т.е. чем ближе величина Н к нулю. Как мы показали выше, это происходит в том случае, когда одно из возможных состояний системы имеет очень высокую вероятность (частоту) проявления. С этих позиций, понятия энтропии можно сравнить с коэффициентом наследуемости (h²), введенным Р.А.Фишером. Чем выше значение коэффициента наследуемости признака в какой-то группе организмов (популяции), тем в меньшей мере уровень проявления этого признака зависит от паратипических факторов, соответственно, тем выше его детерминированность (в данном случае фенотипа генотипом) и, соответственно, ниже энтропия системы.

В своем применении ИЭА в большей мере рассчитан на системы (признаки), имеющие качественное выражение, т.е. для которых различия между отдельными состояниями носит дискретный характер. Однако, как указывает Е.С. Вентцель [12], количественные (или непрерывные) признаки также можно анализировать в терминах и понятиях ИЭА. В этом случае, для всего возможного спектра значений, которые может принять признак, устанавливают некую меру точности (Δх), в пределах которого состояния системы оказываются практически неразличимы. Тогда непрерывно варьирующую систему можно приближенно свести к дискретной. Это равносильно замене плавной кривой функции плотности распределения f(x) ступенчатой ломаной (по типу гистограммы). В этом случае площади прямоугольников этой гистограммы изображают вероятность принятия системой того или иного состояния. Характерно, что оценка энтропии для количественного признака оказывается совершенно не зависящей от принятой меры точности (Δх). От точности измерения зависит только начало отсчета, при котором вычисляется энтропия.

Если система (признак) имеет нормальное распределение (идеальное), то в этом случае ее энтропия, рассчитанная по гистограмме, будет равна:

где σ – среднее квадратичное отклонение анализируемого признака.

Как правило, при сравнении признаков, имеющих различные величины измерения (кг, г, %, см и т.д.), они предварительно подвергаются стандартизации. В этом случае каждое исходное значение в выборке (x_i) заменяют соответствующей z-величиной:

Характерной особенностью этих трансформированных величин является то, что они имеют среднее арифметическое значение равное 0, а вариансу (и, соответственно, среднее квадратичное отклонение), равную 1:

Вне зависимости от того, чему были равны минимальное и максимальное значения в исходной выборке, для z-трансформированных величин подавляющее большинство значений располагаются в пределах от –3 до +3 (рис. 1).

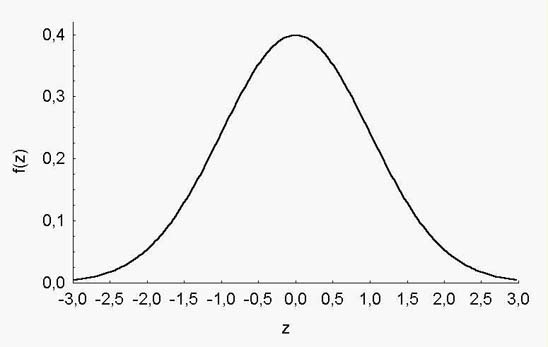
Рис. 1. График плотности распределения стандартизированных величин

В этом случае (при достаточном объеме выборки, содержащей сотни измерений), удобнее принять величину меры точности одинаковую для всех признаков и равную Δх = 0,5. Это дает нам 12 интервалов в пределах вариационного ряда. Таким образом, мы принимаем, что k = 12. И вместо плавной графика плотности распределения f(z) мы имеем дело со ступенчатой гистограммой (рис.2).

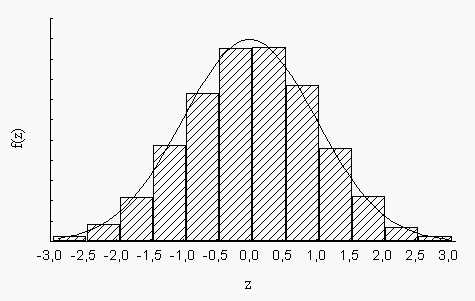
Рис. 2. Гистограмма выборочного распределения с кривой нормального распределения

Энтропия для такой системы (количественного признака) может быть рассчитана по формуле:

где z_i – середина каждого из 12 интервалов, а f(z_i) – функция плотности распределения (относительная частота) для соответствующего значения z_i.

Однако в таком случае мы сталкиваемся с одним важным противоречием. По определению понятия энтропии максимальное возможное значение степени организованности такой системы равно (используя формулу 2):

Но, с другой стороны, согласно формуле 4, для идеального нормального распределения, плотность которого оценена по гистограмме с 12 интервалами, эта величина составляет:

Более того, имеется другое, еще более важное противоречие. Дело в том, что любой количественный признак имеет тип распределения более или менее близкий к нормальному (Гаусса-Лапласа):

когда p = q = 0,5 и n имеет порядок тысяч или десятков тысяч.

С другой стороны, формула 11 описывает частоты генотипов для диаллельной системы в случае ко-доминирования. И в этом случае, величина n соответствует числу пар одновременно учитываемых генов. Если, например, мы рассматривает один ген, то частоты, с которыми будут формироваться фенотипы, будут равны – 1:2:1. Если учитывается два гена одновременно, частоты соответствующих фенотипов будут равны: 1:3:3:1 и т.д. Таким образом, идеальное нормальное распределение соответствует случаю популяции, имеющей максимально возможный уровень гетерозиготности. И только в этом случае уровень дезорганизованности системы (ее энтропия) по определению достигает максимума.

Для того чтобы решить эти противоречия, мы предлагаем следующий выход.

Предлагается оценивать энтропию не для величин плотности распределения z-трансформированных значений исходной выборки, а для интеграла этих оценок, т.е. использовать величины:

График интеграла плотности нормального распределения приведен на рисунке 3.

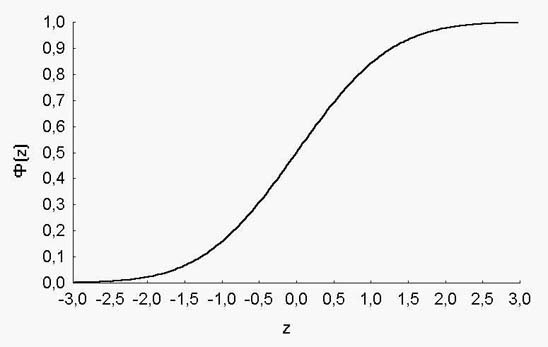
Рис. 3. Кривая интеграла плотности нормального распределения

Что нам дает этот подход.

Во-первых, новые величины – Ф(z) – для любых признаков (имеющие любую размерность) будут варьировать в пределах от 0 до 1. При этом снимается вопрос о выборе нижней границы первого интервала гистограммы. Эта точка всегда равна нулю.

Во-вторых, использование интеграла плотности нормальной кривой приводит к ее сглаживанию; эта особенность интеграла плотности нормального распределения очень часто используется в прикладном статистическом анализе, например, при пробит-анализе [14]. Сглаживание нормальной кривой дает одно важное преимущество, а именно, ее монотоность, т.е. одинаковую величину приращения частоты встречаемости вариант в выборке при увеличении абсолютных значений этих вариант.

Таким образом, гистограмма распределения величин Ф(z) будет иметь следующий вид (рис.4). Следовательно, значения интеграла плотности распределения признака будут иметь равномерное распределение. И это распределение будет тем идеальнее приближаться к равномерному, чем ближе исходное эмпирическое распределение к нормальному.

Как известно, для равномерного распределения, изображенного в виде гистограммы с числом интервалов, равным k, энтропия равна значению, приведенному в формуле 2. А это значит: чем ближе распределение исходного признака к нормальному, тем ближе распределение интеграла его плотности к равномерному и, следовательно, энтропия такой системы будет стремиться к своему максимуму. И, наоборот, чем сильнее эмпирическое распределение исходного признака отклоняется от нормального, тем сильнее будет отклоняться от равномерного распределение интеграла его плотности и, соответственно, тем ниже будет значение энтропии этой системы. В крайнем случае, когда все варианты в выборке (или популяции) будут равны, энтропия такой системы, как и следует по определению, будет равна нулю.

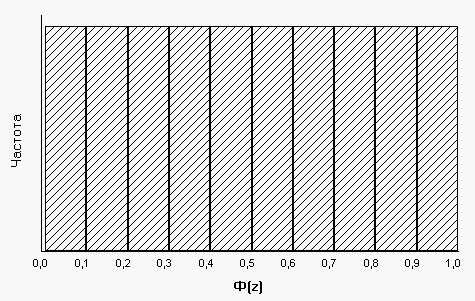
Рис. 4. Гистограмма распределения величин интеграла плотности нормального распределения

Число интервалов, на которое можно разбить отрезок [0;1] для интеграла плотности распределения (т.е. k), зависит от объема выборки. Мы можем предложить такое оптимальное число интервалов, при котором средняя частота попадания величины в любой из них не будет меньше 5-10. Таким образом, для выборок, объемом 100-200 объектов (особей) оптимальным будет 10 интервалов. В этом случае, максимальное значение энтропии такой системы будет равно Hmax = log₂ 10 = 3,322 бита. При бóльшем объеме имеющихся выборочных данных, число интервалов может быть увеличено. При меньшем объеме, наоборот, уменьшено (например, до 5).

Поскольку, оценка энтропии производится на основе случайной выборки, то эта оценка имеет свою статистическую ошибку, зависящую, прежде всего, от объема выборки (n):

Кроме непосредственных оценок энтропии, могут быть также использованы показатели, производные от нее.

Для определения меры абсолютной организации системы используется величина:

Величину относительной организованности системы оценивают по формуле:

Согласно классификации С.Бира [15], система для которой R≤0,1 является вероятностной (стохастической); если значение относительной организованности системы R>0,3, то такая система считается детерминированной. И, наконец, система, для которой 0,1<R≤0,3, является квазидетерминированной (вероятностно-детерминированной).

Кроме того, при проведении ИЭА может быть использована величина, именуемая анэнтропия [16]. Эта величина удовлетворяет функции, которая может служить мерой редкости частот событий:

Величина анэнтропии будет тем выше, чем меньше частоты встречаемости редких вариант в выборке. В том случае, когда частоты встречаемости всех вариант наиболее минимальны (и равны между собой, соответственно), оценка анэнтропии равна нулю. При неравенстве частот вариант, она тем выше, чем реже встречаются самые редкие варианты.

Данная методика, использующая интегральные оценки плотности распределения стандартизированных величин, была применена нами для ИЭА возрастной динамики живой массы орнитологических объектов. Полученные результаты свидетельствуют о перспективности использования данного метода для описания любых количественных признаков биологических объектов.

СПИСОК ЛИТЕРАТУРЫ

1. Меркурьева Е.К., Бертазин А.Б. Применение энтропийного анализа и коэффициента информативности при оценке селекционных признаков в молочном скотоводстве // Доклады ВАСХНИЛ. 1989. № 2.
2. Коваленко В.П., Дебров В.В. Использование энтропийного анализа для прогноза комбинационной способности линий птицы // В кн.: Новые методы селекции и биотехнологии в животноводстве. Ч.2. Репродукция, популяционная генетика и биотехнология. Киев, 1991.
3. Рябоконь Ю.А., Сахацкий Н.И., Кутнюк П.И., Катеринич О.А. Информационно-статистический анализ менделирующих и полигенных признаков в популяциях сельскохозяйственных птиц. Харьков, 1996.
4. Казаков В.Н., Кузнецов И.Э., Герасимов И.Г., Игнатов Д.Ю. Информационный подход к анализу низкочастотной импульсной активности нейронов рострального гипоталамуса // Нейрофизиология. 2001. Т.33, № 4.
5. Козупица Г.С., Ратис Ю.Л., Ратис Е.В. Информационно-энтропийный подход к определению здоровья // Вестник Балтийской академии. 1999. Вып. 25.
6. Герасимов И.Г. Энтропия биологических систем // Проблемы старения и долголетия. 1998. Т.8, № 2.
7. Савинов А.Б. Методология системно-кибернетического подхода в экологическом мониторинге // В кн.: Экологический мониторинг. Ч.4. Н.Новгород: Изд-во ННГУ, 2000.
8. Савинов А.Б. Метод биоиндикации экосистем по соотношению адаптивных и инадаптивных потенциалов популяций и биоценозов (Информационно-энтропийный аспект) // В кн.: Методы популяционной биологии. Сборник материалов VII Всероссийского популяционного семинара. Ч.1. Сыктывкар, 2004.
9. Шеннон К. Работы по теории информации и кибернетике. М.: ИЛ, 1963.
10. Шмальгаузен И.И. Кибернетические вопросы биологии. Новосибирск: Наука, 1968.
11. Эшби У. Введение в кибернетику. М.: ИЛ, 1959.
12. Вентцель Е.С. Теория вероятностей. М.: Гос.изд-во физ.-мат. литературы, 1962.
13. Митропольский А.К. Техника статистических вычислений. М.: Гос.изд-во физ.-мат литературы, 1961.
14. Урбах В.Ю. Биометрические методы. М.: Наука, 1964.
15. Бир С. Кибернетика и управление. М.: ИЛ, 1963.
16. Петров Т.Г. Информационный язык RHA для описания, систематизации и изучения составов многокомпонентных объектов // Научно-техническая информация. 2001. № 3.

S.S.Kramarenko

Nickolaev state agrarian university

The various applications of the entropy-information analysis for quantitative trials of biological objects, having normal distribution are analyzed. It’s shown that more is grounded use of not frequencies of absolute signs, calculated on base histogram of sample’s distribution, and distribution probabilities integral frequencies of z-score.