Вперед К следующему разделу Назад К предыдующему разделу Конец К концу разделу Список К оглавлению

Часть III. Иерархический дисперсионный анализ качественных признаков

5. Иерархический ДДА диморфных признаков

Иерархическая структура ДА возникает в том случае, когда нет полной сочетаемости всех градаций, например, фактора А со всеми градациями, например, фактора В. Структуру полного двухфакторного (crossed 2-way ANOVA) ДА и иерархического в случае двух факторов (nested 2-way ANOVA) ДА можно схематически представить следующим образом:

ДДА

  

И(2)ДА
 

В1

В2

В3

В4

В5

    

В1

В2

В3

В4

В5

В6

А1

Х

Х

Х

Х

Х

  

А1

Х

Х

Х

      

А2

Х

Х

Х

Х

Х

  

А2

      

Х

Х

Х

В представленной выше схеме первая градация фактора А сочетается только с градациями фактора В – В1, В2 и В3, а вторая градация фактора А – только с градациями фактора В – В4, В5 и В6. Сочетаний типа А1×В5 не может существовать вообще в природе ввиду, например, их пространственной и временной разобщенности. Подобная схема структуры ДА возникает, например, в том случае, когда проводятся исследования в двух регионах. В одном регионе анализируется частота встречаемости данного признака в трех популяциях (1-3), и в другом – в трех других популяциях (4-6). Соответственно, просто физически не может быть сочетания первого региона и пятой популяции.

Более сложная иерархическая система может содержать несколько уровней организации, но с обязательным соподчинением ниже стоящих уровней выше стоящим. Например, отдельные демы могут входить в состав популяций, которые, в свою очередь, входят в состав локалитов, которые всвою очередь расположены в различных регионах и т.д. и т.п.

Из других терминов, которые встречаются в русскоязычной литературе для обозначения ИДА, можно привести следующие определения – гнездовой план ДА или план ДА с группировкой.

При проведении иерархического ДДА (ИДДА) для качественных признаков с двумя альтернативными вариациями (диморфными признаками) основная последовательность вычислений остается без изменения, некоторые модификация используются только для расчета частных факториальных варианс и дисперсионных отношений. В этом случае факториальная варианса состоит из двух компонент – вариансы между градациями фактора А () и вариансы между градациями фактора В в пределах градаций фактора А (). Таким образом, сумма этих двух компонент () представляет собой долю изменчивости признака между градациями фактора В между градациями фактора А.

Рассмотрим алгоритм расчета ИДДА на следующем примере.

В двух регионах была проанализирована частота встречаемости формы окраски раковины pallescens наземного моллюска Cepaea vindobonensis. При этом, в пределах каждого региона исследовалось по четыре отдельные популяции.

Нам необходимо выявить, имеются ли различия частоты встречаемости данного признака для улиток, обитающих в различных регионах и между популяциями в пределах разных регионов?

Все исходные данные приведены в таблице 5.1.

Таблица 5.1
 

А1

А2

Суммы

В1

В2

В3

В4

В5

В6

В7

В8

m

13

17

15

10

45

50

35

15

M = 200

n

150

125

225

250

275

300

275

150

N = 1750

p

0,087

0,136

0,067

0,040

0,164

0,167

0,127

0,100

= 0,114

CZ

11,915

14,688

14,065

9,600

37,704

41,733

30,490

13,500

  

1. После того, как рассчитаны частные частоты для каждой выборки и средняя частота встречаемости данного признака во всей совокупности (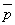= 0,114) мы можем перейти оценке суммарной и остаточной варианс:

,

(5.1)

,

(5.2)

где b – число градаций фактора В (т.е. совокупное число исследованных популяций и в первом, и во втором регионах).

Тогда факториальна варианса (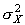) может быть оценена как разность между суммарной и остаточной:

.

(5.3)

Как мы уже указывали выше, эта компонента представляет собой сумму:

,

(5.4)

поэтому, рассчитав одно из этих значений, второе можно получить простым вычитанием.

2. Частную факториальную вариансу (), вызванную влиянием фактора А (т.е. различиями по регионам) вычисляем на основании данных, суммированных для всех популяций в пределах каждого региона (табл. 5.2).

Тогда, искомая величина может быть найдена по формуле:

,

(5.5)

где а – число градаций фактора А.

Таблица 5.2

 

А1

А2

mА

55

145

nА

750

1000

pА

0,073

0,145

СА = n·pА·(1 - pА)

50,753

123,975

Тогда частная факториальная варианса (), вызванная влиянием фактора В в пределах фактора А, будет равна:

.

(5.6)

3. Число степеней свободы для каждой компоненты изменчивости дисперсионного комплекса рассчитываются по следующим формулам:

dfT = N – 1;

(5.7)

dfA = a – 1;

(5.8)

dfB(А) = b – а;

(5.9)

dfX = b – 1;

(5.10)

dfZ = N – b.

(5.11)

Таким образом, соответствующие значения числа степеней свободы будут равны: dfT = 1749; dfA = 1; dfВ(А) = 6; dfX = 7 и dfZ = 1742.

4. Средние квадраты рассчитываются стандартно, как отношения варианс к соответствующим значениям числа степеней свободы; например, для фактора А значение среднего квадрата будет равно:

и т.п.

(5.12)

5. Как уже указывалось выше, в случае проведения ИДДА принципиально меняется правило расчета факториальных отношений. Для нашего примера они рассчитываются по следующим формулам:

;

(5.13)

.

(5.14)

Тогда итоговая таблица ДА будет иметь следующий вид (табл. 5.3).

Таблица 5.3

Источник
изменчивости

s 2

df

MS

F

p

А

2,029

1

2,029

11,80

0,014

В(А)

1,033

6

0,172

1,72

0,113

X

3,062

7

0,437

4,37

<0,001

Z

173,695

1742

0,100

T

176,757

1749

Таким образом, отвергается нуль-гипотеза только в отношении региональной изменчивости по частоте признака (с уровнем значимости p = 0,014), тогда как в пределах своих регионов популяции оказываются гомогенными.

Оценку силы влияния факторов, использованных в анализе, можно провести, как обычно, двумя способами.

Первый способ. В этом случае оценки силы влияния фактора рассчитывается как отношение соответствующей факториальной вариансы к суммарной:

;

(5.14)

.

(5.15)

Уровень значимости этих оценок определяется на основе сравнения величин

,

(5.16)

(5.17)

с табличным значением критерия Хи-квадрат с соответствующим числом степеней свободы (формулы (5.7) и (5.8)).

Формулы (5.14)-(5.17) применимы в случае, когда b ≥ 12-16 (особенно, первая из них).

Второй способ основывается на разложении оценок факториальных средних квадратов.

Вначале необходимо рассчитать величины:

;

(5.18)

;

(5.19)

,

(5.20)

где

.

(5.21)

Тогда компоненты соответствующих средних квадратов можно найти по формулам:

;

(5.22)

;

(5.23)

.

(5.24)

А оценки силы влияния факторов А и В(А):

;

(5.25)

,

(5.26)

где

.

(5.27)

Для данных из нашего примера соответствующие величины будут равны:

;

;

;

;

; ;

.

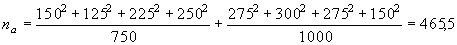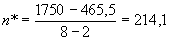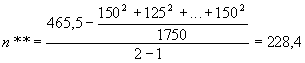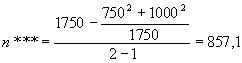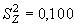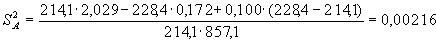Тогда оценки силы влияния факторов А и В(А) будут равны:

;

.

* * *

Кроме обычных оценок силы влияния фактора, организация иерархического ДДА позволяет также найти важные оценки, которые часто используются при проведении анализа генетической изменчивости с использованием алгоритма ДА (Weir, Cockerham, 1984; Yang, 1998).

Меру изменчивости популяций между регионами оценивает показатель:

,

(5.28)

меру изменчивости признака между популяциями в пределах рассматриваемых регионов оценивает показатель:

,

(5.29)

и, наконец, меру изменчивости признака между популяциями между регионами оценивает показатель:

.

(5.30)

Последний показатель очень часто используется в качестве степени дифференциации популяций при проведении популяционно-генетических исследований.

Для данных из рассматриваемого примера эти оценки будут равны, соответственно: FCT = 0,0033; FSC = 0,0022; FST = 0,0244.

Вперед К следующему разделу Назад К предыдующему разделу Начало К концу разделу Список К оглавлению